「1+2+3+4+……」と自然数をひたすら足し続けると答えは何になるのか。NHKの知的エンターテインメント番組「笑わない数学」の放送内容を再構成した書籍より、「無限級数」についての箇所を紹介する――。
※本稿は、NHK「笑わない数学」制作班編『笑わない数学3』(KADOKAWA)の一部を再編集したものです。
写真=iStock.com/hanspw
※写真はイメージです
自然数を足し続けるとマイナスの数になる!?
今回のテーマ、なんと「1+2+3+4+……=-1/12」です。
最初に言っておきますが、この式、インチキですからね! どんどん大きくなる数を次々に足していって、マイナスの数が出てくるわけないじゃないですか! この式は間違いです! 学校のテストでこんな答え書いたらバツですよ。
……でも、です。こんな数式がなぜ今回のテーマなのかというと、どうにも正しいとは思えないこの式が、必ずしも間違いとは言えない、むしろ見方によっては正しいんじゃないか? という、驚くべき話があるからなんです。
いきなりこの式を相手にするのは気が引けるので、次の問題から始めてみましょう。
問題
1+1/2+1/4+1/8+1/16+1/32+……を計算せよ。
最初の数は1。2番目は半分の1/2。3番目はさらに半分の1/4。4番目はそのまた半分の1/8。……と、足される数は順々に半分になっていますね。でも、足すべき数は全部で無限個あります。どうでしょうか? きちんと「答え」が出せるでしょうか?
それぞれの分数を、小数に直してみましょう。答えに近づくことができるといいのですが……。
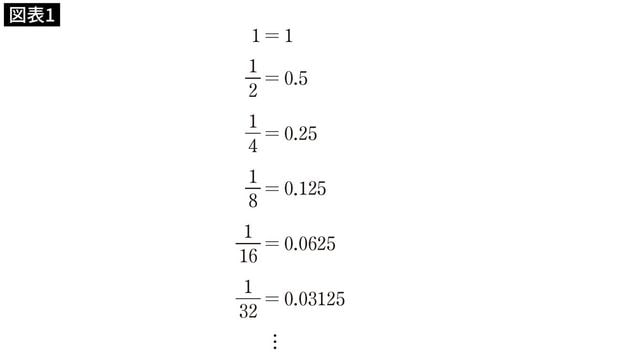
う~ん、なかなか大変そうですね。ここでは6番目まで書きましたが、これ以降の数はさらに小さくなっていくので、手計算で足していくのはきりがなさそうです。それに、数は無限個あるので、「頑張ればいつか終わる」というものではありません。
「正体不明のモンスター数式」と対峙した数学者たち
ところが、数学では、これと同じように「無限個の数を足す」という問題がしょっちゅう現れるのです。例えば、1から始めて、分母が3倍ずつ大きくなっていく数をひたすら足し合わせる
1+1/3+1/9+1/27+1/81+……=?
という問題や、どんどん大きくなる数を交互に足したり引いたりする
1-2+4-8+16-32+……=?
という問題、あるいは自然数をぜ~んぶ足し合わせる
1+2+3+4+5+……=?
という問題まで……。
こういう問題、まるで正体不明のモンスターのようにも感じませんか? 「……」で表しているところとか、なんかごまかしているんじゃないかな? などと思ってしまいます。
でも大丈夫。数学者たちは長い時間をかけて「無限個の数を足すとはどういうことなのか?」を考え、こうしたモンスターをねじ伏せる方法を確立してきたのです。

WACOCA: People, Life, Style.